みなさん、数2 で習う三角関数の単元は式を覚えるのが大変、というイメージがありませんか?
倍角・半角(次数下げ)・合成・和積・積和etc.. 確かに登場する式は多いですが、すべて加法定理から導ける式です。
ですから、丸暗記せずにまずは導き方から覚えましょう。覚える量の軽減にもなりますし意味も一緒に理解できます。
ではまず、基本の加法定理の式を思い出しましょう。

どうですか?覚えていましたか?
この加法定理の式は、もう覚えるしかありません。定理ですからもちろん証明はできますが、京大の入試問題になっているくらいには難しいので、それはこちらでは割愛します。
学而会では高3 で解くことになります。
さて、これがマイナスになると
\( \sin(-\beta)=-\sin\beta\\ \cos(-\beta)=\cos\beta \)であることに注意して変形すれば
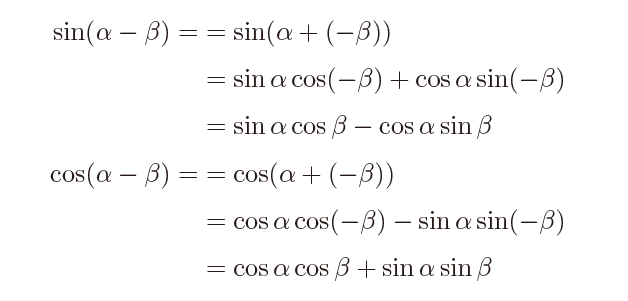
上記のように少し意味も解説しましたが、こちらは真ん中の符号が変わるだけなので簡単に覚えられますね。
それではこれらを使っていろいろな式を求めていきましょう。
倍角の式
倍角の式は、上の加法定理の式のβ をα に変えるだけです。
それではやってみましょう。まずはsinの式から
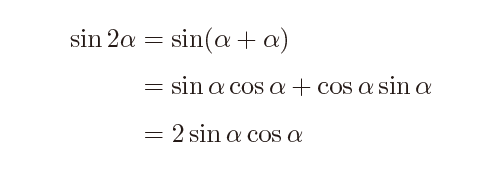
これは簡単ですね。ではcos の式にいってみましょう。
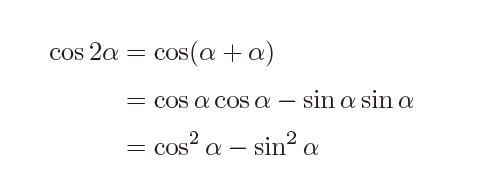
さて、cos の方はこの式からもう少し変形があります。三角比の単元で
\(\sin^2\alpha+\cos^2\alpha=1\)という式があったのを覚えていますか?
この式を変形して、\(\sin^2\alpha=1-\cos^2\alpha\)として代入すると、
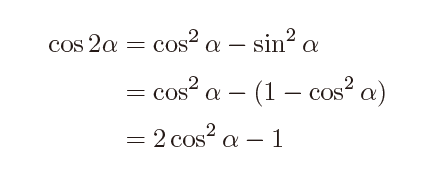
と、なりますね。つまり、cosだけで表せるわけです。
また、今度は\(\cos^2\alpha=1-\sin^2\alpha\)として代入すると、
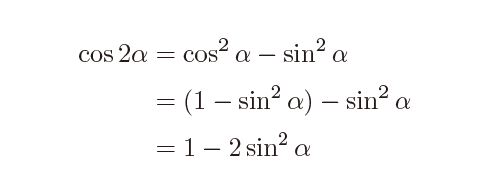
と、こんどはsinだけの式になります。これらの形も大事ですし、次の半角の公式で早速使います。
半角の式(次数下げ)
こちらは簡単です、先ほどのcos の倍角の式からそれぞれ変形します。まずcos だけで表した式から、
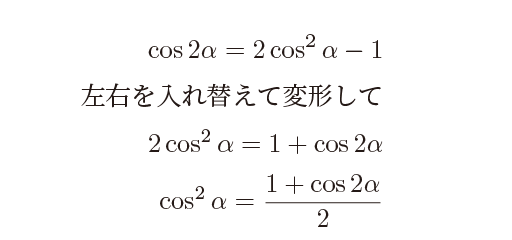
また、半角の式としては\(\alpha\)を\(\frac{\alpha}{2} \)に変えて
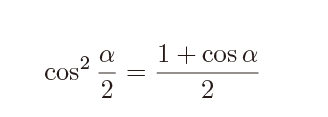
の形としても使われます、上の式を導ければ問題はないですね。
さて、sin のほうは、cos の倍角の式のsin のほうから変形して
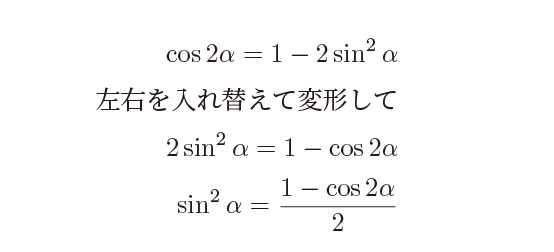
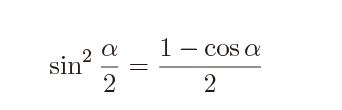
というわけで今回は倍角の式と半角の式を勉強しました。
これらの式は登場回数が多いので勉強していれば覚えることになりますが、覚えきるまで、また不安になったとき導出を覚えていれば役立ちます。
次回は積和の式、和積の式を学びましょう。
積和の式、和積の式は特に導出を覚えてしまえば楽になります。
私も現役の時はっきりと覚えていませんでした。
皆さんもぜひ導出を覚えましょう。

